大阪大学基礎工学部機械工学同窓会Alumni Association of Department of Mechanical Engineering

【非線形力学領域・垂水 竜一 教授】

結晶欠陥の表裏一体関係の起源
－柔らかい幾何学による並進・回転欠陥の新しい見方－

・並進と回転を特徴とする二つの異なる結晶欠陥（※1）の間に指摘されてきた等価性の起源を解明

・これまで、二つの欠陥を包括する理論的枠組みの整備は十分進められておらず、両者に同等のひずみ場が現れる根本的なメカニズムは未解明だった

・柔らかい幾何学「リーマン・カルタン多様体（※2）」に基づく統一理論の整備を進め、この課題を解決

・両者を幾何学的な共通の物差しで整理することが可能となり、近年注目されている回位による材料強化を理解する土台としての応用に期待

大阪大学大学院基礎工学研究科の小林舜典助教、大学院生の武政勝己さん（当時博士前期課程）、垂水竜一教授らの研究グループは、結晶中の「刃状転位」と「くさび回位」が等価なふるまいを示す仕組みを明らかにしました。両者は、規則的な原子配列からなる結晶に含まれた不規則な欠陥構造です。

欠陥の周囲に生じるひずみ場は結晶の強度や靱性を左右するため、材料科学分野での重要な研究対象とされています。これまで、一列に並んだ刃状転位の端部にくさび回位と同等のひずみ場が現れることは知られていましたが、その根本的なメカニズムは不明でした。

今回、研究グループは空間を柔軟にゆがませることのできる幾何学「リーマン・カルタン多様体」に基づく結晶欠陥理論の整備を進め、両者がアフィン接続（※3）と呼ばれる幾何学的構造のみで区別され、それ以外の骨組みが同一となることが、ひずみ場の等価性の起源であることを明らかにしました。さらに、同じ考え方は単独の刃状転位にも適用でき、正負のくさび回位双極子モーメントとして再解釈できることが分かりました。本成果は、優れた特性を持つ新しい結晶材料の設計方針に活用できると期待されます。

本研究成果は、英国科学誌「Royal Society Open Science」に、7月16日（水）8時（日本時間）に公開されました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

【用語説明】
（※1）結晶欠陥
理想的な結晶は規則的な原子配列からなるが、現実的には原子配列の規則性を破る様々な欠陥が多数内在している。原子配列の並進対称性を破る転位と、回転対称性を破る回位はその代表例である。いずれも対称性の破れた領域が線状に連なった線欠陥に分類される。

（※2）リーマン・カルタン多様体
平坦なユークリッド空間でのベクトルの内角（計量）と平行移動操作（アフィン接続）を一般化した空間の一種で、微分幾何学という数学を土台としている。空間の幾何学的な特徴は捩率と曲率という構造に代表される。結晶欠陥理論への応用は我が国の研究者である近藤一夫や甘利俊一らによって1950年代から進められた。この空間では転位を捩率、回位を曲率として表現することができる。

（※3）アフィン接続
リーマン・カルタン多様体上のベクトルの平行移動を記述する幾何学的構造。通常の平坦なユークリッド空間では、ベクトルを平行移動しても向きも大きさも変わらないが、リーマン・カルタン多様体上ではこれらが変化しうる。アフィン接続がその特性を決定している。

Last Update : 2025/07/31

【非線形力学領域・垂水 竜一 教授】

跳ねるおもちゃがパチンと鳴る仕組み
－次世代のソフトロボット技術に活用－

・半球状シェル構造が跳躍する仕組みを明らかにしました

・跳躍過程において，基盤との接触状態が跳躍性能の予測に重要であることがわかりました

・接触状態が遷移する様子を捉えることで最大跳躍高さや跳躍条件を予測することに成功しました

・ソフトロボットの構成要素を詳細に解析することで，その性能予測が可能になる事が示唆されます

慶應義塾大学大学院理工学研究科の阿部宝(研究当時修士課程2年)，中原行健(博士課程1年)，同大学理工学部機械工学科の高橋英俊准教授，石上玄也教授，佐野友彦専任講師，大阪大学大学院基礎工学研究科の橋口勲武(博士課程3年)，小林舜典助教，垂水竜一教授らによる研究グループは，薄い半球状のシェル構造が跳躍する仕組みを明らかにしました。

　近年，ソフトロボットが開発されていますが，ソフトロボットの挙動は材料特性や環境との複雑な相互作用に影響されるため，性能の予測が困難であり，経験的な設計が必要でした．本研究では，跳躍するおもちゃ(ポッピンアイ)に着想を得て，跳躍ソフトロボットの基本構造の１つである半球状シェル構造の跳躍性能を解明しました．跳躍性能を予測式によって理論的に計算できる本研究成果は，未知環境におけるソフトロボットの設計指針に示唆を与えることが期待されます。本研究は2025年6月9日に国際科学雑誌「Advanced Robotics Research」で公開され，刊行号の裏表紙を飾りました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

Last Update : 2025/07/02

【生体工学領域・小林 洋 准教授】

人の筋肉を使って複雑な計算ができる！
－ウェアラブルシステムなどへの応用に期待－

・人の生体組織（筋肉）を用いて、複雑な計算ができる
 ことを発見

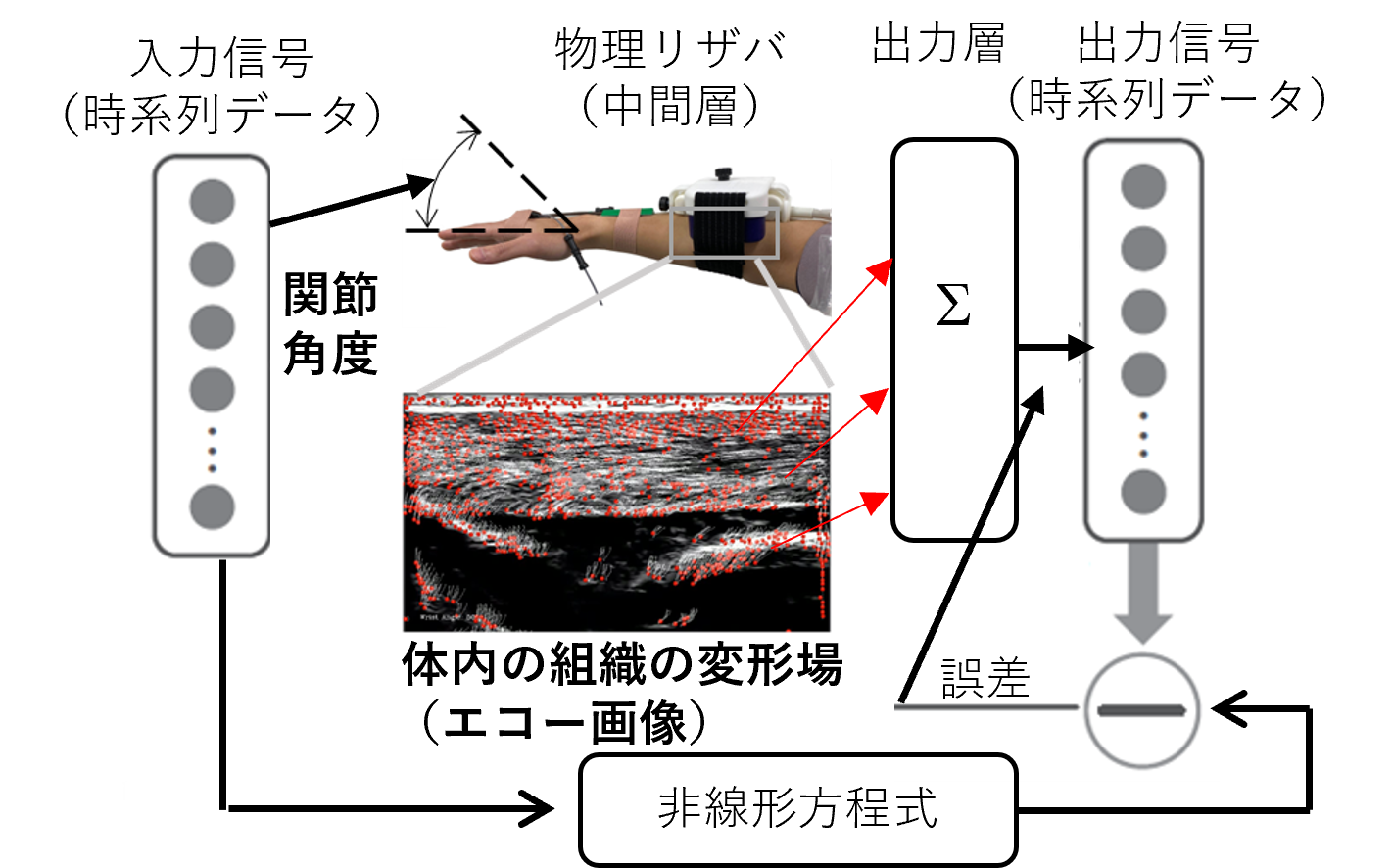
・人の生体組織（筋肉）の変形場を物理リザバコンピュ
 ーティング（※1）の中間層として利用できることを
 実証

・物理的な計算機が不要で、人の近くのあらゆる場所で
 計算処理を提供できることから、ウェアラブルシステ
 ムなどハードウェアレスな計算機への応用に期待

大阪大学大学院基礎工学研究科の小林洋准教授は、人の生体組織（筋肉）を利用して複雑な計算が可能であることを世界で初めて明らかにしました。

物理系の力学を利用して、複雑な計算問題を効率的に解決する計算手法を「物理リザバコンピューティング」と呼びます。これまで、物理リザバコンピューティングの中間層（リザバ層）として、光学系、力学系、量子系などさまざまなものが利用されてきましたが、人の組織を利用した例はありませんでした。

本研究では、人の生体組織の変形場を物理リザバコンピューティングのリザバ層として利用することを提案し、その実証として複雑な方程式を解くことに成功しました。これらのことは、人の組織が計算能力を有することを示しています。

これらの技術は、人の組織というその場にあるものを利用するため、ハードウェアレスな構成となり、人の近くのあらゆる場所で計算処理を提供できます。将来的に、ウェアラブルシステムなどへの応用が期待されます。

本研究成果は、米国科学誌「IEEE　Access」に、２０２５年３月２０日付けで掲載されました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

【用語説明】
（※1）物理リザバコンピューティング
物理リザバコンピューティングは、物理系の力学を利用して、複雑な計算問題を効率的に解決する計算手法です。従来のリザバコンピューティングのアプローチを物理現象に適用したものです。例としては、光学系、力学系、量子系などの物理的なシステムを「中間層（リザバ層）」として活用し、データ処理を行う手法です。物理リザバコンピューティングでは、情報処理は中間層となる物理系が担うため、対象とする計算を行う際、原理的に他の計算機を必要としません。

Last Update : 2025/04/18