HOME > 研究室だより

研究室だより Vol.6　河原研究室

非線形力学領域　熱流体力学講座　熱工学グループ

乱流の骨格
―単純不変解による乱流へのアプローチ―

教授・河原 源太

水や空気などの流体の運動状態は層流と乱流に大別されます。乱流状態では時間的にも空間的にも流れは複雑に乱れ、同じ運動が繰り返されることはありません。水道の蛇口から勢いよく流れ出す水流や煙突から立ち上る煙の渦運動など、日常生活で目にする流れのほとんどは乱流です。

乱流の問題は物理学における未解決の難問のひとつとして広く知られており、その解明は理学的にも工学的にも重要な意義をもちます。乱流が難問とされる理由はいくつかありますが、なかでも、乱流の示す複雑でカオス的な時空間構造の本質をいかにして簡潔に表現するか、は大きな課題です。

最近、我々は、この問題の解決に向け、独自の理論的アプローチを試みています。それは、乱流を支配する運動方程式であるナビエ・ストークス方程式の単純な不変解を用いて、乱流の構造や統計的性質を表現しようとするものです。

単純不変解とは、時間的に変化しない定常解や、同じ運動が繰り返される周期解といった解であり、複雑で多様な乱流に比べ、はるかに簡潔です。この不変解を用いれば、乱流中に隠された単純で秩序をもつ構造やその乱流統計量との関連性を運動方程式に忠実に表すことができます。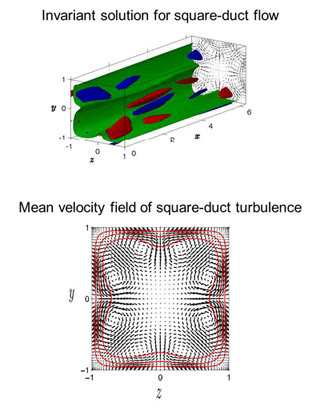

単純不変解の一例を図（上）に示します。これは、断面が正方形であるダクトに沿って圧力差で駆動される流れの定常（進行波）解です。図中に赤と青で示した渦構造がダクトの軸に垂直な流れを誘導し（ベクトル線図）、軸方向の速度成分の分布（緑の等値面）を歪ませます。この不変解は、図（下）に示す正方形ダクト乱流の平均速度分布の特徴をうまく再現しています。

単純不変解は、乱流よりもはるかに単純であるにも拘わらず、その時空間構造や統計的性質をよく再現するという意味で、「乱流の骨格」をなすと言えるでしょう。現在、我々はこの乱流の骨格を用いて、乱流の解明と制御に取り組んでいます。

河原研究室ホームページ　http://www-thermomech.me.es.osaka-u.ac.jp/

Last Update : 2015/05/13