HOME > 研究室だより

研究室だより Vol.23　垂水研究室

【非線形力学領域・垂水 竜一 教授】

結晶の中で力が生まれるメカニズム
―柔らかい幾何学を用いた材料科学の新しい理論―

・微分幾何学（※1）を用いてらせん転位（※2）の周辺に形成される力学場を解析

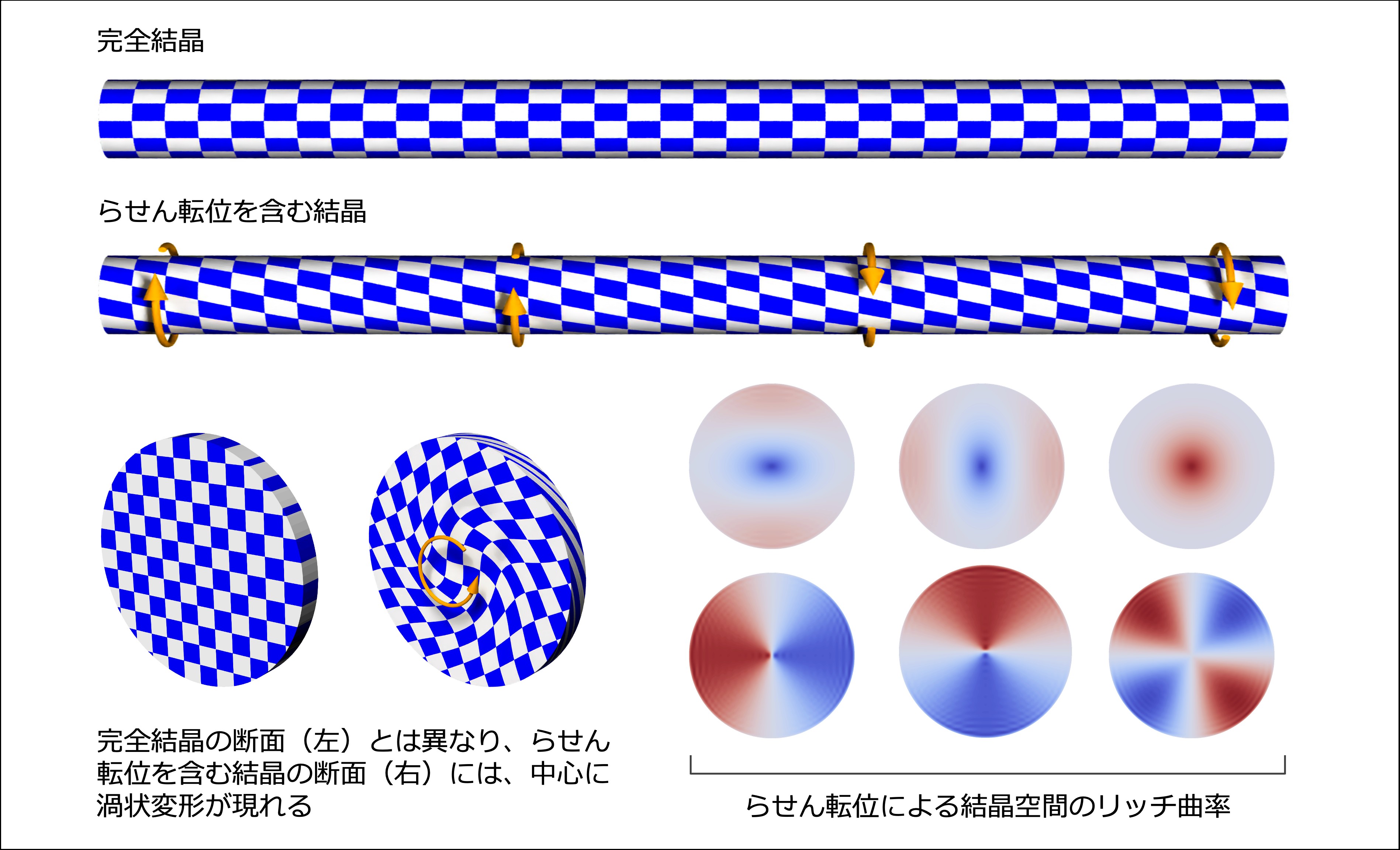
・転位による結晶格子のゆがみは空間のリッチ曲率（※3）を表しており、これが結晶の中に力を生み出す直接的な起源となる

・結晶材料の強度・延性向上のための新しい理論として広範な応用展開が可能

 

大阪大学大学院基礎工学研究科の小林舜典助教と垂水竜一教授は、らせん転位によって生み出される結晶格子の乱れが結晶格子の中で力へ変換されるメカニズムを数学的に解明しました。らせん転位は結晶材料の強度や延性を決定する重要なトポロジカル欠陥の一つですが、その力学的な性質に関する研究は十分進んでおらず、多くの研究課題が残されていました。
今回、垂水教授らの研究グループでは、らせん転位の理論解析に微分幾何学を用いることによって、(i)らせん転位の中心には「リッチ曲率」と呼ばれる結晶空間のゆがみが存在すること、(ii)リッチ曲率は通常の結晶空間（ユークリッド空間）と非整合な「幾何学的なフラストレーション（※4）」状態を生み出すこと、(iii)フラストレート状態の解消に必要な弾性変形が力の起源となること、を明らかにしました。

 


本研究の成果は、2024年12月4日（水）に英国王立協会誌「Royal Society Open Science」により公開されました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

 

【用語説明】
（※1） 微分幾何学
微分操作を通して対象の形の特徴（幾何学）を調べる分野のこと。例えば、曲線や曲面の曲がり方の指標（曲率）を数式で表すことができる。物理学では微分幾何学を使って理論を記述する例が多く、その代表例の一つがEinsteinの重力理論である。
（※2）らせん転位
結晶に見られる原子配列の乱れの一種で、らせん階段に似た結晶格子の乱れを引き起こす。物理的にはVolterra欠陥、数学的には一次元トポロジカル欠陥の一種と考えることができる。
（※3）曲率
微分幾何学で用いられる、空間の曲がり方を表す指標の一つ。一例として、球の表面は半径に反比例した一定の曲率を持つと考えられる。この研究では、らせん転位が生み出す結晶のゆがみをリッチ曲率として評価した。
（※4）幾何学的なフラストレーション
通常、フラストレーション状態とは系がエネルギーの最安定状態を取ることができず、準安定的な状態に留まることを指す。ここでは転位による結晶空間のリッチ曲率が、本来のユークリッド空間とは幾何学的に不整合となり、そのため弾性変形を伴う準安定的な状態にあることを意味している。

Last Update : 2025/04/18